在几千年人类漫漫科学史上，为了争夺荣誉发生的巨大争斗的事件比比皆是，而牛顿和莱布尼茨之争是数学史上最精彩的纷争之一。而争论的焦点是，关于微积分的发明权归属问题。

要了解整个纷争的前因后果，我们先把时钟调到17世纪。

17世纪之前，有若干学者在研究中都有意无意地涉及到了“求切线”和“求曲线下的面积”的问题。最早可以追溯到古希腊时期，17世纪的英国数学家巴罗把求曲线的切线与求曲线下区域的面积问题联系了起来。站在后世的角度看，巴罗已经站在了微积分的门槛上。但可惜的是，他没能从一般概念的意义下进一步深入地研究它们。

到了17世纪中叶，一场轰轰烈烈的科学革命拉开序幕，而数学作为各种学科描述自然的工具却开始遇到了瓶颈。

这一时期，人们关注变量与一般曲线的研究；在力学上，人们关心如何根据路程去确定瞬时速度，或者根据瞬时速度去求路程；在几何上，人们希望找到求一般曲线的切线的方法，并计算一般曲线所围图形的面积……

这些看似不同领域的问题却归结为相同模式的数学问题，那就是求因变量在某一时刻对自变量的变化率，以及因变量在一定时间过程中所积累的变化。前者导致了微分的概念；后者导致了积分的概念，两者都包含了极限与无穷小的思想。而首次科学、系统地研究微积分的人，是大名鼎鼎的科学家牛顿。

牛顿在科学界是什么地位？他是物理学家、数学家、哲学家，同时应该还兼任神学家，在中国物理课本和数学课本上随便翻几页就能看到他的名字，被称为是“现代科学的开山鼻祖”。

1666年，他在计算月球轨道涉及到的向心力时，发明了流数术，这可以看作后来微积分的前身；1669年用拉丁文写成《运用无限多项方程的分析》，即《分析学》；1671年完成了《流数法与无穷级数》，即《流数法》。

不过，他只是把微积分当做自己随手使用的简便算法，这些论文也并未公开发表，只是在朋友之间传看。牛顿一直对自己的成果秘而不宣，有人猜测他是担心发布新论文会给自己引来麻烦，还不如自己在书房里自行研究；也有人猜测牛顿嫌自己目前的体系还不完善，希望完善后再进行发表。但这一决定，实质上给他后来带来了大麻烦。

当时，牛顿并不是在当时唯一一个对微积分进行系统研究的人，同一时代，莱布尼茨也在对微积分进行研究。莱布尼茨是何许人？他是德国数学家，物理学家，哲学家，被誉为十七世纪的亚里士多德。

不知是英雄所见略同还是传闻中的剽窃，这两个科学界的天才都对微积分进行了研究。

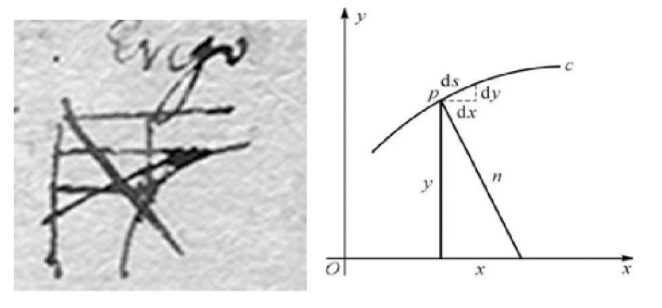
有证据表明莱布尼茨曾和牛顿进行过关于微积分的通信，其中两封最重要的牛顿回函如今被称作“前函”与“后函”。在这两封信中，牛顿一方面担心莱布尼茨窃取自己首创的微积分思想，另一方面却又要彰显微积分的首创之权。两封信遮遮掩掩而疑心重重，他提到了自己在研究“流数”，为了防止自己的首创权旁落，牛顿只是谨慎地按照学术惯例，留下了一段难解的密码：6accdae13eff7i319n404qrr4s8t12vx，其大概的涵义是：“已知包含若干流量的方程，求流数；或者反过来，已知流数，求流量。”

这段语焉不详的文字，是公开信函中最早关于微积分的定义。在“后函”中，牛顿听闻莱布尼茨在信件中提到的与自己体系有异但内核一致的微积分体系，看着莱布尼茨的信函，他不算客气地评价道：“以前悬而未决的问题现在同样无解。”

牛顿在同莱布尼茨通信后依然没有选择马上发表自己的微积分科学成果。而在1684年，莱布尼茨在莱比锡《教师学报》上发表了论文《一种求极值和求切线的新方法，亦能应用于分数和无理量情形及非寻常类型的有关计算》。尽管全文只有6页，且理论尚不成熟，论证也不太严谨，却具有里程碑般的重要历史意义，因为这是数学史上第一篇正式发表的微分学文献。

莱布尼茨对1673年以来自己对微分学研究进行概括总结，着重介绍了微分定义、运算法则及曲线的极值、拐点等问题。两年后，他又在《教师学报》发表了另一篇论文——《论一种深奥几何学与不可分量及其无穷分析》。

该文以讨论积分学为主，谓之《新方法》续篇。在这两篇论文中，莱布尼茨都声称，自己的微积分方法是独立探索出来的，并没有提到牛顿的名字。

牛顿对此非常愤怒，莱布尼茨在论文中根本不提自己的名字就敢发表自己近二十年前的研究成果，这在牛顿看来是学术剽窃的不道德行为。除此之外，莱布尼茨的论文非常粗糙，其关注的要点是在讨论微积分的应用，很多数学上的基础问题还真如牛顿的信件中所说的那样“悬而未决”。发表这样的半成品，不仅是学术剽窃，更是无视科学规范的行为，无论如何，牛顿不想“就这么算了”。

不过当时的牛顿在欧洲大陆的影响力还不够，没有立即对莱布尼茨的论文给予反驳。一年半后，牛顿划时代的巨著《论自然哲学的数学原理》正式出版，在第二册中，他特别增加了一段叙述，提到了之前与莱布尼茨“前函”与“后函”的通信，陈明自己才是微积分的最早发明人。当年牛顿与莱布尼茨的“前函”与“后函”，如今成为了牛顿一方指责莱布尼茨剽窃的重要证据。

在牛顿的支持下，英国皇家学会对莱布尼茨发起了如潮的舆论攻势，而莱布尼茨在1711-1712年连续两次提出言辞激烈的抗议，表达对牛顿的不满；皇家学院之外，莱布尼茨更是和其他支持他的科学家联手写下匿名传单，寄送给全欧洲各大学术机构，表达是自己发明了微积分。

在他看来，牛顿只是自己在研究流数法而已，还将其禁锢在书房中不对外发表，也拒绝与同行进行细致探讨。而自己不但将微积分首次展现在大家面前，还为其设计了一套微积分的符号表示法，这比牛顿的“点记法”不知道高到哪里去了。事实上，今天世界上的高等数学课本中提到的微积分符号，的确是从莱布尼茨的符号得来的。

同时，莱布尼茨认为，自己一直在研究微积分，在知道牛顿也在进行同一领域的研究后，就迅速与对方取得联络。然而牛顿只是回复了两封遮掩的信函，还把结论藏在一堆密码里。自己没有从牛顿处得到帮助，发表了虽不完善但对整个数学界都有启发的论文，当然不必提牛顿的名字。在这种情况下，牛顿竟然联合整个英国皇家学会对自己进行打压，连自己对皇家学院的控诉函都置之不理，自己当然要在全欧发匿名传单来有所回应。但牛顿在欧洲的科学界地位如日中天，莱布尼茨的嗟叹也无济于事。

最终，莱布尼茨于1716年郁郁而终，而牛顿比莱布尼茨多活了13年，去世时享尽哀荣。两位微积分的发明人先后撒手人寰，但他们各自探索出的微积分却遗泽至今。

微积分的诞生具有划时代的意义，它是高等数学的标志，是数学史上的分水岭与转折点，是人类思维最伟大的成就之一。

这个伟大发明所产生的新数学与旧数学有本质的区别：旧数学是关于常量的数学，新数学是关于变量的数学；旧数学是静态的，新数学是动态的；旧数学只涉及固定的和有限的量，新数学则包含了运动、变化和无限。

18世纪被称为数学史上的英雄世纪。数学家们把微积分应用于天文学、力学、光学、热学等各个领域，获得了丰硕的成果。在数学本身，他们把微积分作为工具，又发展出微分方程、微分几何、无穷级数等理论分支，大大扩展了数学研究的范围。

如今，科学界公正地将牛顿和莱布尼茨同时视为微积分的发明人，既承认牛顿先于莱布尼茨发明了微积分，也承认莱布尼茨与牛顿的发明是彼此独立不存在互相借鉴。今天的大学课本里还使用着莱布尼茨的记号体系，两个人的成果最终为全人类所共享。