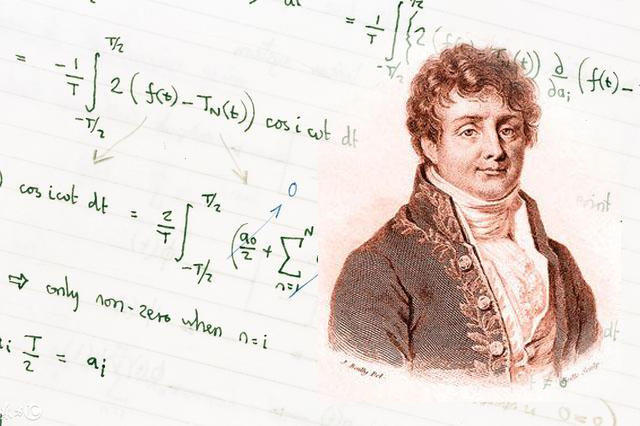
不仅是一个数学工具,傅里叶变换更是一种能彻底颠覆一个人世界观的思维模式。
傅里叶变换不仅是一个数学工具,更是一种可以彻底颠覆一个人以前世界观的思维模式。但不幸的是,它的公式看起来实在是太复杂了。
数学意义上的傅里叶变换(Fourier transform),用通俗易懂的话来讲,就是“将一切的函数用正弦函数拟合”。因其基本思想首先由法国学者约瑟夫·傅里叶系统地提出,所以以其名字来命名以示纪念。
1807年,时年39岁的法国数学家傅里叶在法国科学学会上展示了一篇论文。在论文中展示了一个极具争议性的论断,那就是:“任何连续周期信号可以由一组适当的正弦曲线组合而成”。
在当时,法国的另外两位数学家拉普拉斯和拉格朗日都注意到了傅里叶的这篇论文,但他们两人对此意见不一:拉普拉斯赞成傅里叶的观点,而拉格朗日则对这个观点持有反对的态度。两位法国数学界的泰斗因为这篇论文差点撸起袖子干一架,傅里叶只好先把这篇论文束之高阁。
隔了15年之后,1822年,傅里叶才出版了一部关于物理学的作品——《热的解析理论》。这部著作在物理上的贡献是热传导的偏微分方程,但在论文中傅里叶有机会将自己“用正弦函数拟合所有函数”的数学理论加以阐释。

约瑟夫. 傅里叶的画像
傅里叶在论文中声明,一个变量的任意函数,不论是否连续或不连续,都可展开为正弦函数的级数,而这正弦函数的参数为变量的倍数。虽然从严格的数学意义上讲,傅里叶当时的这个结论缺乏证明且不严谨,但后来德国数学家狄利克雷证明了在有限制的条件下,傅里叶的结论是对的。
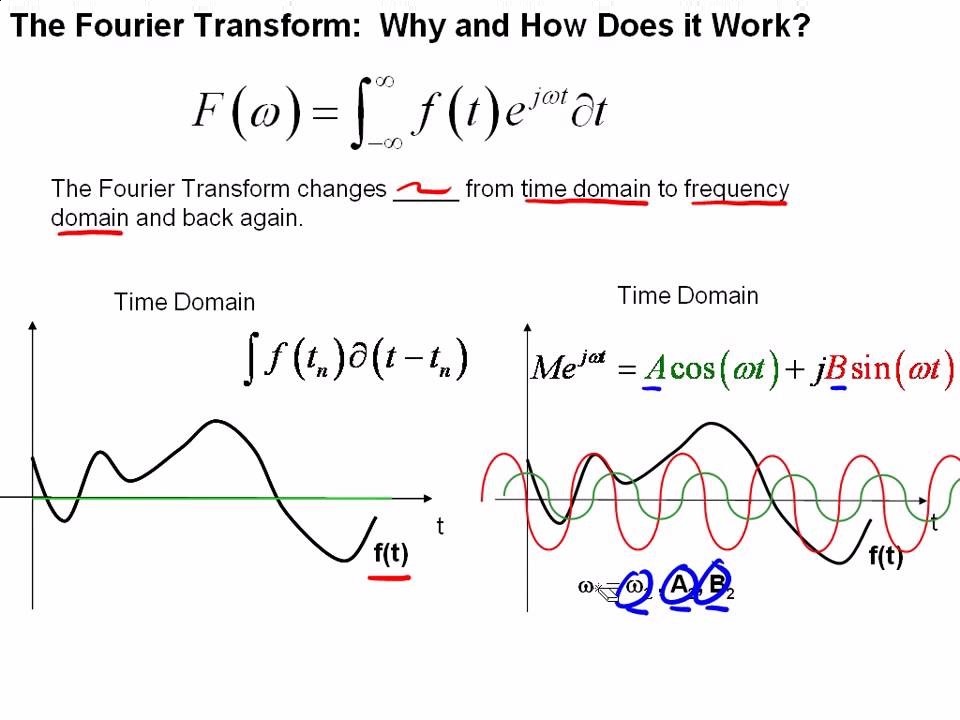
傅里叶变换的直观示意图,在图中,一个任意的函数被拆解为几个正弦函数的叠加
1830年5月16日,傅里叶病逝于巴黎。一年后,他的遗稿被整理出版成书,后人将傅里叶的论断进行了扩展:满足一定条件的函数可以表示成三角函数(正弦和/或余弦函数)或者它们的积分的线性组合。在这种条件下,虽然有限数量的正弦曲线的确无法组合成一个带有棱角的信号,然而,无限数量的正弦曲线的组合从能量的角度可以非常无限逼近带有棱角的信号。这样,傅里叶变换从数学的角度就被建立起来了。
傅里叶变换是将任意函数用正弦函数的叠加拟合。进入20世纪,随着电子工业的发展,人们需要用电子设备通过数学函数的方式拟合自然信号的时候,傅里叶选择正弦函数的优越性就体现了出来。
正弦波输入至线性系统,不会产生新的频率成分,正弦波输入至任何线性系统,出来的还是正弦波,改变的仅仅是幅值和相位。用单位幅值的不同频率的正弦波输入至特定线性系统之后,记录其输出正弦波的幅值和频率的关系,就得到该系统的幅频特性,记录输出正弦波的相位和频率的关系,就得到该系统的相频特性。
换句话说,只要研究正弦波的输入输出关系,就可以知道该系统对任意输入信号的响应。从这个意义上讲,傅里叶的伟大之处不在于如何进行傅里叶变换,而是在于给出了“任何连续周期信号可以由一组适当的正弦曲线组合而成”这一论断。知道了这一论断,只要知道正弦函数的基本特性,一个非常复杂的信号也是可以被傅里叶变换处理,拆解成正弦函数的。
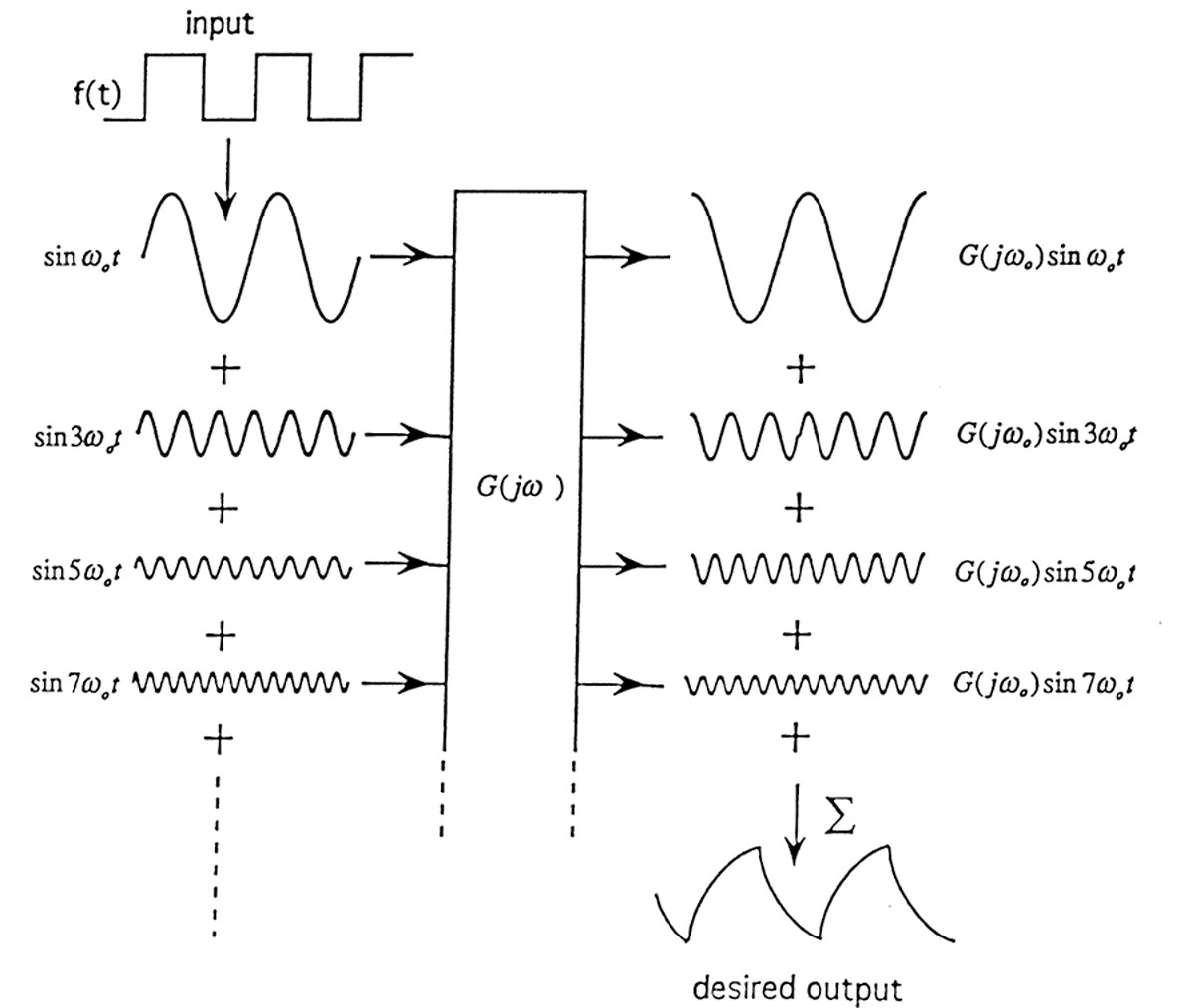
几个正弦函数的叠加得到一组典型的信号尖峰
而现代通信中为了表示二进制所经常使用的方波,其实可以用傅里叶变换拆解成有限个或无限个正弦函数的叠加。在这种情况下,处理信号的响应,阈值等问题时,可以将其简化为简单的三角函数波形处理。这在一定意义上奠定了“模拟信号”向“数字信号”进化的理论基础。
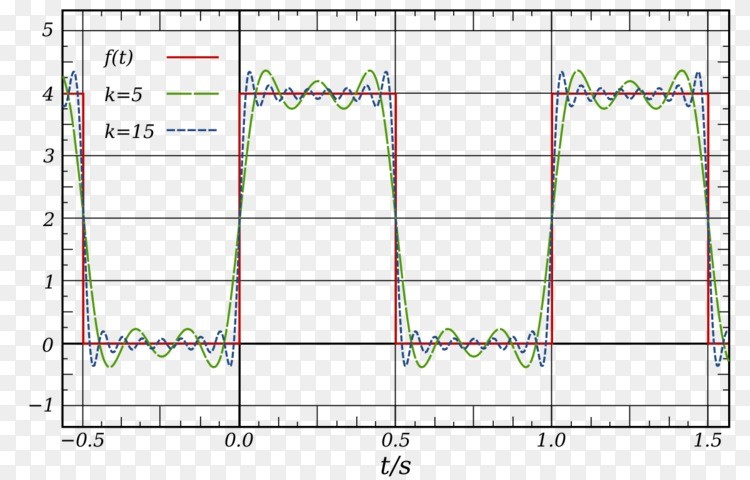
用正弦曲线叠加方波
傅里叶变换是有史以来最伟大、最深刻的数学发现之一。它发现于19世纪早期,得到大规模工程技术的应用却要等到20世纪了。那时,通信和信号处理构成了电子时代的基石,而傅里叶变换作为通信和信号处理的理论基础,也被赋予了“电子时代数字内核”的地位。

位于法国格勒诺布尔的傅里叶大理石胸像
20世纪初,意大利人马可尼发现无线电波可以承载信号,而无线电波就是一种典型的正弦波,所以针对无线电波的操作,比如信号的加密,截获,等等,其底层的数学运算都是以傅里叶变换为基础的;
随着无线电通信的发展,傅里叶变换已经成为了工程技术人员通用的数学语言;
进入数码时代以后,虽然对于通信工程师和软件工程师而言,编写程序的语言已经愈发的人性化,但信号传输的机器底层也还是靠着正弦波和方波来进行的。这些方波信号的设计,一则是基于二进制的计算机思维,二则也是离不开傅里叶变换当中方波和正弦波的转换处理。在这一百多年,每一个电信物理上的重大发明,其背后也都有傅里叶变换的影子。

位于法国巴黎拉雪兹神甫公墓的傅里叶墓地
如今,作为数学史上的重大发现,傅里叶变换和相关的傅里叶级数,已成为每个大学理科工科学生在学习高等数学或者数学分析课程时的必修课。